《运筹学》实验指导
《运筹学》实验指导
前言
运筹学实验的课程,目的是通过学习实际问题的数学模型建立,用软件求解操作培养学生的逻辑思维,掌握基本的定量分析知识,有利于专业的知识储备。本实验指导共6项实验,分别从软件的使用、线性规划问题、运输问题、网络分析方面实际问题指导学生操作,实验过程中要求学生能分析实际问题、对学生实验操作、独立思考等起到指导作用。
实验教材:自编教材
实验学时:12学时
实验一 LINGO或excel的线性规划求解
(综合性实验,1学时)
【实验目的与要求】
1.使学生掌握线性规划建模的方法以及至少掌握一种线性规划软件的使用,提高学生应用线性规划方法解决实际问题的实践动手能力。
2.通过实验,使学生更深入、直观地理解和掌握线性规划的基本概念及基本理论和方法。3.要求学生能对一般的线性规划问题建立正确的线性规划数学模型,掌握excel或lingo线性规划模块的操作方法与步骤,能对求解结果进行简单的应用分析。
【实验仪器、器材与试剂】
无
【实验内容、方法与步骤】
1.选择合适的线性规划问题,学生可根据自己的建模能力,从本实验指导书提供的参考选题中或从其它途径选择合适的线性规划问题。
2.建立线性规划数学模型。学生针对所选的线性规划问题,运用线性规划建模的方法,建立恰当的线性规划数学模型。
3.用excel或lingo求解线性规划数学模型
4.对求解结果进行应用分析
步骤:
.一、了解excel规划求解的原理
“规划求解”是 Excel 中的一个加载宏,借助“规划求解”,可求得工作表上某个单元格(被称为目标单元格)中公式(公式:单元格中的一系列值、单元格引用、名称或运算符的组合,可生成新的值。公式总是以等号(=)开始。)的最优值。“规划求解”将对直接或间接与目标单元格中公式相关联的一组单元格中的数值进行调整,最终在目标单元格公式中求得期望的结果。“规划求解”通过调整所指定的可更改的单元格(可变单元格)中的值,从目标单元格公式中求得所需的结果。
2.规划求解的加载
在安装Excel时,只有在选择[完全/定制安装]时才可选择装入这个模块。
(1)安装完成进入Excel后,在[工具]菜单(如下图所示)中点击加载宏选项之后,
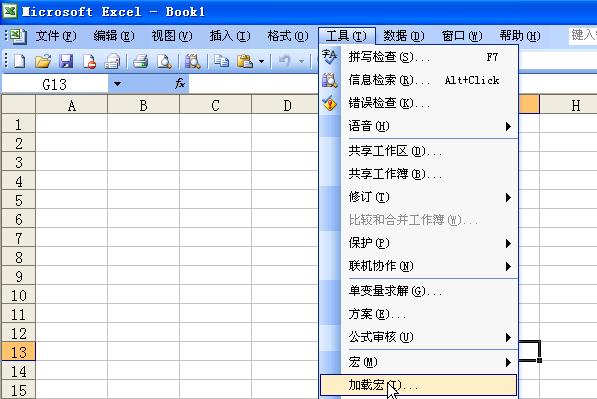
在弹出的对话框中的“可用加载宏”列表框中,选定待添加的加 载宏“规划求解”选项旁的复选框,然后单击“确定”。单击“确定”以后,“工具”菜单下就会出现一项“规划求解”。如果需要其他功能,也可以用鼠标勾选(加载的宏越多,excel 启动的时候就会越慢,所以请根据自己的需要选择)。
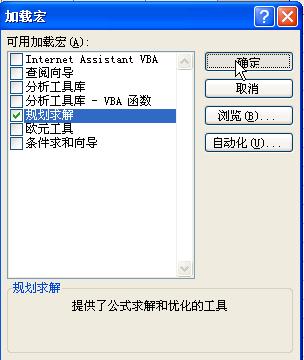
3.规划求解工具的参数说明和设置
用鼠标左键单击〔工具〕菜单中的〔规划求解〕选项,弹出〔规划求解参数〕对话框,对话框参数解释如下:
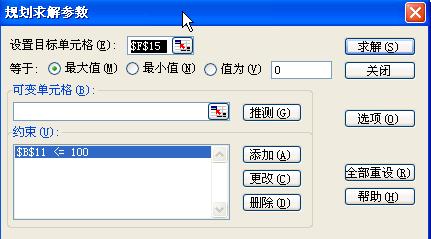
设置目标单元格:一些单元格、具体数值、运算符号的组合。注意:目标单元格一定要是公式,即一定是以“=”开始。类似于线性规划中的目标函数。
等于:最大值、最小值:在此指定是否希望目标单元格为最大值、最小值或某一特定数值。如果需要指定数值,请在右侧编辑框中键入该值。
可变单元格:指决策变量(不含公式)所在的单元格.可以有多个单元格或区域。
推测:单击此按钮,自动推测“设置目标单元格”框中的公式所引用的所有非公式单元格,并在“可变单元格”框中定位这些单元格的引用。
约束:增加、修改、删除各个约束条件(等式或不等式),逐个的增加、修改或删除约束条件。
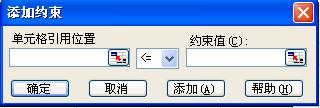
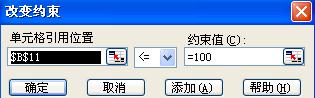
求解:对所设置的问题进行求解。
全部重设:清除所有当前条件,进行重新设置。
选项:在其中可加载或保存规划求解模型,并对求解过程的高级属性进行控制。
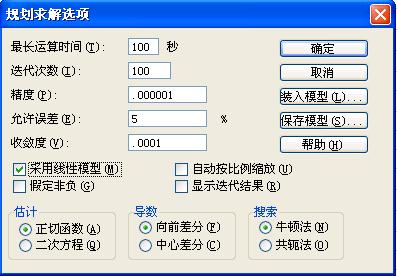
采用线性模型:当模型中的所有关系都是线性的,并且希望解决线性优化问题时,选中此复选框可加速求解进程。如模型是非线性规划或不知道时不选该项,此项可不选。
显示迭代结果:如果选中此复选框,每进行一次迭代后都将中断“规划求解”,并显示当前的迭代结果。
假定非负:如果选中此复选框,则对于在“添加约束”对话框的“约束值”框中没有设置下限的所有可变单元格,假定其下限为 0(零)。
当所有参数都设置完使,点击求解按钮,将显示求解结果,同时可以根据求解结果显示相关敏感分析报告。
保存求解结果:将决策变量的值(可变单元格的取值存在可变单元格的位置)
报告:根据选择的报告自动生成相应的报告,如下表
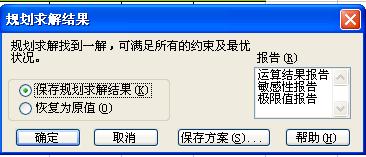
4.规划求解步骤
Max z=2x1+3x2-x3
2x1+2x2+2x3≥12
4x1+x2+2x3=16
2x1+3x2+x3≤5
X1,x2,x3≥0
(1)在工作表上建立模型
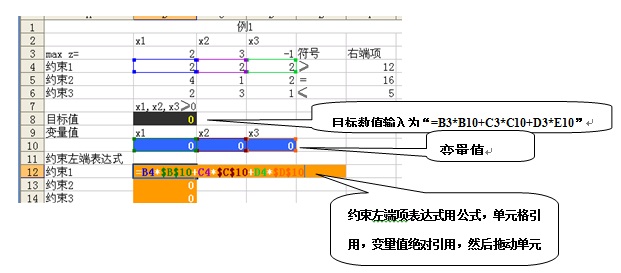
(2)单击“工具”菜单下的“规划求解”,在弹出的“规划求解参数”对话框中输入各项参数。
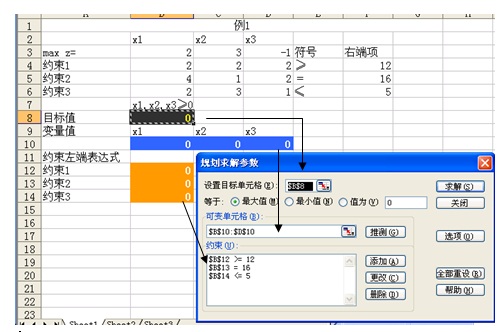
在选项按钮中可以选择求解线性规划和假定非负,点击求解按钮出现下图,选中报告后并保存求解结果:
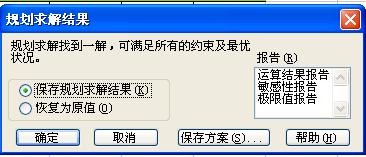
然后根据报告分析解的情况。
二、lingo求解线性规划问题操作
(1)启动lindo系统
启动lindo系统后,出现如下界面:
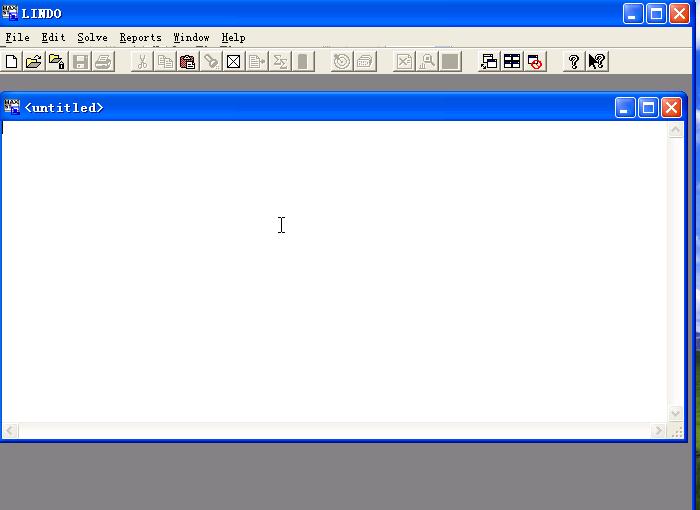
外面的标记有“LINDO”的窗口是主窗口。所有其它窗口将包含在这个窗口内。主窗口还包含所有的命令菜单和命令工具栏。6个主要菜单类:File(文件)菜单、Edit(编辑)菜单、Solve(求解)菜单、Reports(报告)菜单、Window(窗口)菜单)、Help(帮助)菜单。标记有“untitled”的较小的子窗口是一个新的、空白的模型窗口。我们将在这个窗口直接输入示例模型。
(2)以实例1为例练习在空白模型窗口中输入待求解模型
Max z=2x1+3x2
St
10x1+20x2<=80
4x1 <=16
6x2 <=18
X1,x2>=0
1)确定决策变量并输入模标函数
Lindo系统中目标函数只有两种选择:max(最大化)和min(最小化)根据要求解的问题确定是max还是min,然后利用决策变量(在LINDO中,当你在模型使用某个变量的那一刻,它就存在了,你除了在模型中输入它以外,不必做任何事情)表示目标函数表达式。
在空白窗口中输入max 2x1+3x2 后回车
2)确定约束条件
你在目标函数的下一行输入SUBJECT TO(或只是ST),然后回车,并且输入
10x1+20x2<=80
4x1 <=16
6x2 <=18
注意:(1)LINDO将“<”解释为“小于等于”而不是“严格小于”。可以输入“<=”替代“<”字符。
(2)lindo中没有乘号*,如2x1不能写成2*x1。
(3)变量只能出现在不等号的左侧,常数只能出现在不等号的右侧。
(4)lindo默认所有变量非负。
最后,在其后的那一行上,指明约束条件的结束,输入:
END
以上内容输入后,你的屏幕看起来应该是这样:

模型输入完备准备求解。
(3)求解模型
要求解模型,可从Solve(求解)菜单中选择Solve(求解)命令,或按窗口顶部工具栏中的求解按钮(),LINDO将试着编译模型开始。这意味着LINDO将测定模型是否具有数学意义,是否遵循语法的要求。如果模型不通过这些检验,你将被告知如下信息:
An error occurred during compilation on line: n
(在编译期间一个错误发生在:n行)
然后LINDO将跳到发生错误的那一行。你应检查这一行的语法错误并改正它们。
如果在编译阶段期间没有发现模型错误,LINDO将开始实际求解模型。当Lindo的内部求解器启动时,它将在屏幕上显示如下状态窗口(Status Window):
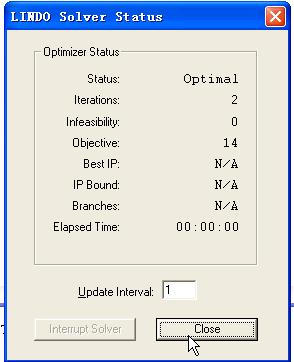
这个状态窗口对于监视求解器的进展是有用的。状态窗口内的各种区域和控制的描述如下。
区域/控制 描述
Status 给出当前解的状态。可能值包括:最佳、可行、不可行、无界
Iterations 求解器的迭代次数
Infeasibility 约束条件被违背的数量(不可行性)
Objective 目标函数的当前值
Best IP 发现的最佳整数解的目标值,仅与整数规划模型相关
IP Bound 对整数规划模型的目标函数的理论约束。仅与整数规划相关
Branches Lindo的整数规划求解器对整数变量分支的数量。仅与整数规划模型相关
Elapsed Time 从求解器被调用开始所经过的时间
Update Interval 状态窗口被更新的频率(按秒)。你可以将其设为所希望的任何非负值。将间隔设为零将增加求解时间
Interrupt Solver 在任何时候按此按钮中断求解器,返回其发现的当前最优解
Close 按此按钮关闭状态窗口。优化将继续。从Window(窗口)菜单选择Status Window(状态窗口)命令,状态窗口可以重新打开
当求解完成时,它将提示你是否进行敏感性和范围分析。
最后,你将能够使用这个信息,但对于现在,按“No”按钮关闭状态窗口。
【实验报告】
以学号姓名实验内容命名,pdf提交。
实验二 线性规划问题的建模与求解
(设计性实验,4学时)
【实验目的与要求】
1. 能在Excel表格中建立线性规划问题的模型;
2. 会填“规划求解”对话框中各项参数内容,并进行正确求解;
【实验仪器、器材与试剂】
无
【实验内容、方法与步骤】
1、在Excel中加载规划求解工具。
2、在Excel中建立线性规划模型数据表。
3、确定需要做出的决策,并指定可变单元格和目标单元格,作好标识。
4、指出约束条件,并将以数据和决策表示的被限制结果放入输出单元格。
5、在“规划求解”对话框中点击“选项”按钮,选“采用线性模型和假定非负”。
6、最后回到“规划求解”对话框,点击“求解”按钮
【实验报告】
以学号姓名实验内容命名,pdf提交。
实验三 灵敏度分析
(设计性实验,2学时)
【实验目的与要求】
1. 能在Excel表格中建立线性规划的模型;
2. 掌握灵敏度分析及其敏感性报告;
【实验仪器、器材与试剂】
无
【实验内容、方法与步骤】
某工厂在计划期内要安排甲、乙两种产品的生产,已知生产单位产品所需成本分别为2千元和3千元;根据产品特性,产品总数不得少于350件,产品甲不得少于125件;又知生产这两种产品需要某种钢材,产品甲、乙每件分别需要钢材2t、1t,钢材的供应量限制在600t。问题:工厂应分别生产多少单位甲、乙产品才能使总成本最低?
解: 容易建立如下线性规划模型。设x1、x2分别为产品甲、乙的产量,模型为
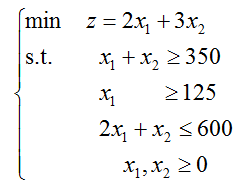
(1) 数据输入:如图1-2所示。
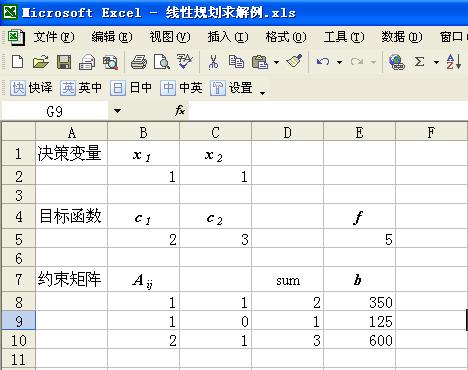
图1-2 数据输入界面
在输入界面中,第1、4、7行是说明文字,无论输入什么内容或不输入均不会影响计算。其中,单元格B2、C2为决策变量初值,对于线性规划求解,初值可任取;B5、C5是目标函数系数;B8、C8、B9、C9、B10、C10为各约束函数的左端系数;E8、E9、E10为约束右端项。以上数据均直接从键盘输入。关键的是,E5、D8、D9、D10分别为目标函数和约束左端三个函数的计算公式。E5的输入如图1-3所示,见红色箭头指示。
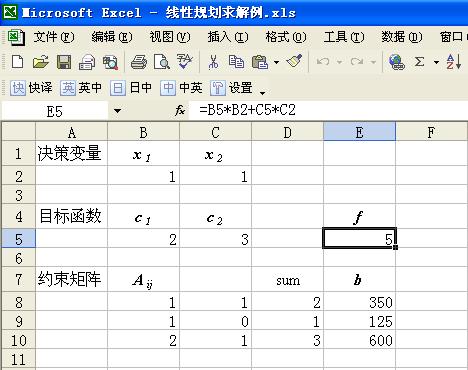
图1-3 E5公式输入方式
D8、D9、D10用同样的方式可以输入:=B8*B2+C8*C2,=B8*B2+C8*C2,=B8*B2+C8*C2。
(2) 调用“规划求解”模块:单击“工具(T)”栏的“规划求解”,得到图1-4“规划求解参数”框。
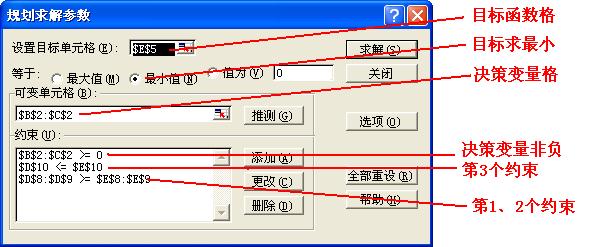
图1-4 规划求解参数框
首先设置目标单元格,这里$E$5即E5。其余设置如图1-4所示,值得说明的是设置可变单元格通过单击“推测(G)”来完成,设置约束通过单击“添加(A)”来完成。
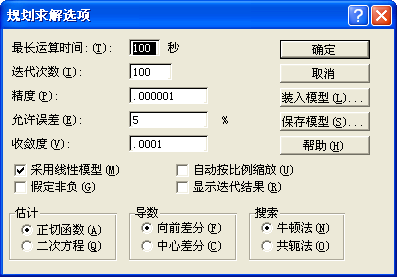
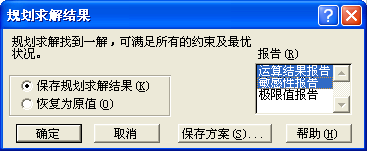
图1-5 规划求解选项框 图1-6 规划求解结果选择框
在这一步要通过单击“选项(0)”来设置有关信息,单击“选项(0)”后可得到如图1-5所示的框。在这里只需单击“采用线性模型(M)”即可完成,然后点“确定”,回到“规划求解参数”框。
(3) 解线性规划模型:在“规划求解参数”框单击“求解(S)”,得到如图1-6所示的“规划求解结果”框,其中“报告(R)”只选“运算结果报告”和“敏感性报告”即可。单击“确定”。
Excel文档中产生两个新表:“运算结果报告”(图1-7)和“敏感性报告”(图1-8)。
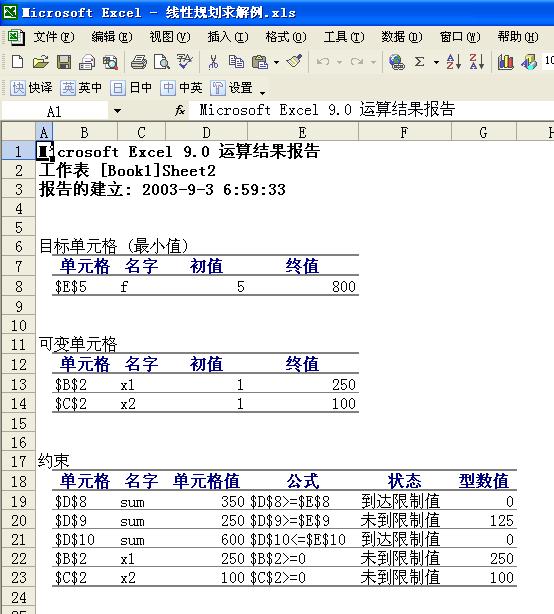
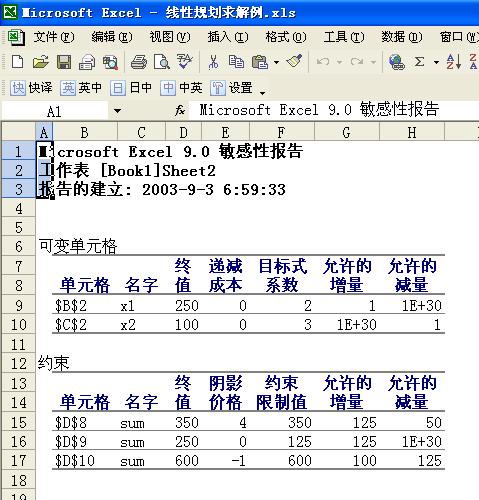
图1-7 运算结果报告 图1-8 敏感性报告
运算结果报告 ( 图1-7 ) 中,列出了线性规划的最优值(800)、最优解(x1=250, x2=100),以及约束松弛变量的值(s1 = 0, s2 = 125, s3 = 0)。
敏感性报告 ( 图1-8 ) 中,列出了线性规划的对偶价格(影子价格、阴影价格4、0、-1);关于目标函数的单因素灵敏性信息:c1当前值为2,当其他参数均不变时,它最多增加1,减少时可趋于负无穷,最优解不会变;c2当前值为3,当其他参数均不变时,它最多增加可趋于正无穷,最多减少1时,最优解不会变;
关于约束右端项:b1当前值为350,当其他参数均不变时,它最多增加125,最多减少50时,对偶价格(影子价格)不会变;b2当前值为125,当其他参数均不变时,它最多增加125,减少时可趋于负无穷,对偶价格(影子价格)不会变;b3当前值为600,当其他参数均不变时,它最多增加100,最多减少125时,对偶价格(影子价格)不会变。
【实验报告】
电子提交课后习题。
实验四 整数规划
(设计性实验,2学时)
【实验目的与要求】
1. 建立实际问题的整数规划模型;
2. 用lingo软件求解;
【实验仪器、器材与试剂】
无
【实验内容、方法与步骤】
1. 建立实际问题的整数规划模型;
2. 用lingo软件求解;
设某部队为了完成某项特殊任务,需要昼夜24小时不间断值班,但每天不同的时段所需要的人数不同,具体情况如表4-4所示。假设值班人员分别在各时间段开始时上班,并连续工作8h。现在的问题是该部队要完成这项任务至少需要配备多少名值班人员?

解:
根据题意,假设用(i=1,2,3,4,5,6)分别表示第i个班次开始上班的人数,
每个人都要连续值班8h,于是根据问题的要求可归结为如下的整数规划模型:
目标函数:
约束条件:

model:
sets:
num/1,2,3,4,5,6/:b,x;
endsets
data:
b=60,70,60,50,20,30;
enddata
[obj]min=@sum(num(i):x(i));
x(1)+x(6)>=60;
x(1)+x(2)>=70;
x(2)+x(3)>=60;
x(3)+x(4)>=50;
x(4)+x(5)>=20;
x(5)+x(6)>=30;
@for(num(i):@gin(x(i));x(i)>=0);
end
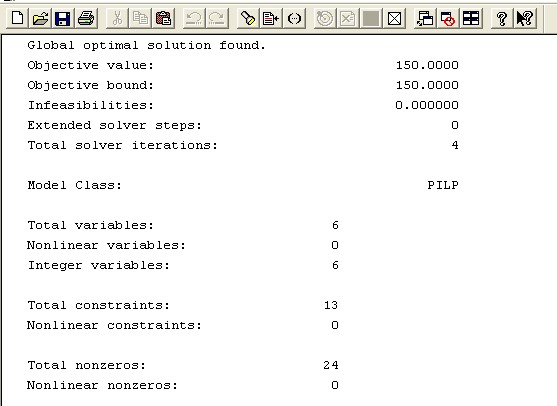
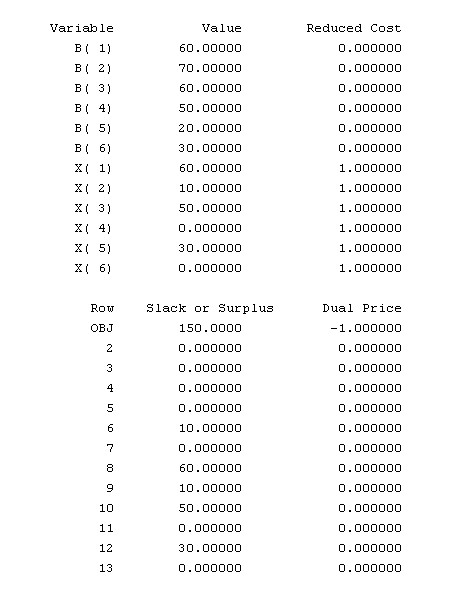
运行该程序得到的结果为:x1=60,x2=10,x3=50,x4=0,x5=30,x6=0。
即值班安排如下:第一班开始上班的人数为60人,第二班开始上班的人数为10
人,第三班开始上班的人数为50人,第五班开始上班的人数为30人,第四和第
六班无需新上班的人,共计需要150人。
【实验报告】
以学号姓名实验内容命名提交pdf电子报告。
实验五 运输问题与指派问题
(设计性实验,2学时)
【实验目的与要求】
1. 能在Excel表格中建立产销平衡问题的模型;
2. 会填“规划求解”对话框中各项参数内容,并进行正确求解;
3.能在lingo建立指派问题的模型。
【实验仪器、器材与试剂】
无
【实验内容、方法与步骤】
运输问题步骤:
1.在Excel中加载规划求解工具。
2.在Excel中建立运输问题数据表。
3、确定需要做出的决策,并指定可变单元格和目标单元格,作好标识。
4、指出约束条件,并将以数据和决策表示的被限制结果放入输出单元格。
5、在“规划求解”对话框中点击“选项”按钮,选“采用线性模型和假定非负”。
6、最后回到“规划求解”对话框,点击“求解”按钮。
案例、某食品公司下设三个加工厂和各厂产量分别为A1——7t ,A2——4t,A3——9t,将这些产品运往4个销售地区及每天的销售量分别为B1——3t,B2——6t,B3——5t,B4——6t,问如何调运,使在满足各销售地区销售量的情况下,总运费最小?运价表见图1。

图1
建立规划求解方案与求解的步骤如下:
F1:F3填产量表,A5:D5填售量表,A7:D9填运价表。见图2。
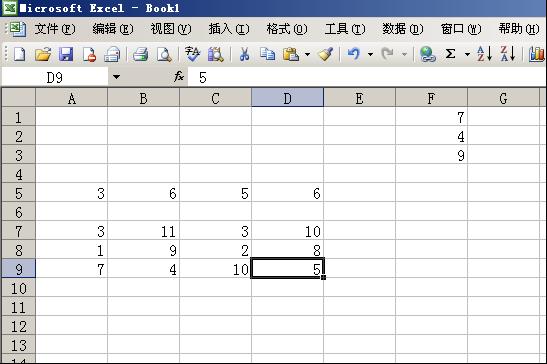
图2
E1填=SUM(A1:D1),并复制到E3;A4=SUM(A1:A3),并复制到D4;A6=SUMPRODUCT(A1:D3,A7:D9)。见图3。
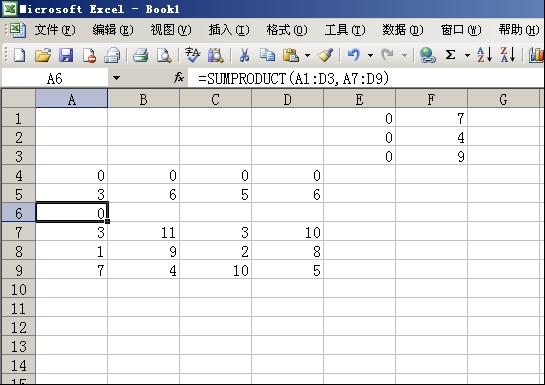
图3
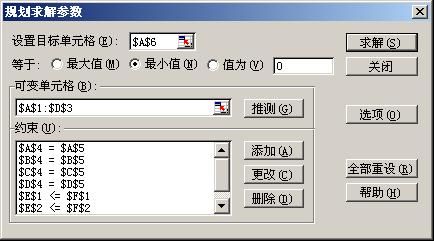
3、 启动规划求解:设置目标单元格:$A$6 等于:最小值
可变单元格:$A$1:$D$3,约束:A4=A5, B4=B5, C4=C5, D4=D5, E1<=F1, E2<=F2, E3<=F3在 选项 中选中:采用线性模型,假定非负。见图4.
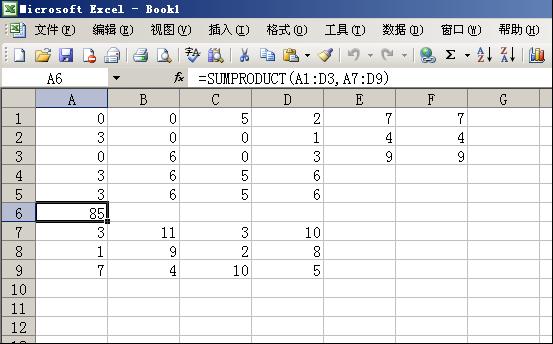
求解。得到答案:总运价为85,调运方案为:
A1给B3调运5t,B4调运2t,A2给B1调运3t,B4调运1t
A3给B2调运6t,B4调运3t。见图5。
四、实验内容。
用电子表格求解下属运输问题:某公司设有A,B,C三个加工厂,产量分别为:9吨、5吨、7吨;有甲,乙,丙,丁四个销售点,销量分别为:3吨、8吨、4吨、6吨;从各工厂到销售点的单位产品的运价为左表所示,问该公司应该如何调运产品使总运费最少?
| 甲 | 乙 | 丙 | 丁 |
A | 2 | 9 | 10 | 7 |
B | 1 | 3 | 4 | 2 |
C | 8 | 4 | 2 | 5 |
D | 3 | 8 | 4 | 6 |
指派问题:lingo完成
设有n个人, 计划作n项工作, 其中表示第i个人做第j项工作的收益,求一种指派方式,使得每个人完成一项工作,使总收益最大.现6个人做6项工作的最优指派问题,其收益矩阵如表所示,请给出合理安排.
人 | 工作1 | 工作2 | 工作3 | 工作4 | 工作5 | 工作6 |
1 | 20 | 15 | 16 | 5 | 4 | 7 |
2 | 17 | 15 | 33 | 12 | 8 | 6 |
3 | 9 | 12 | 18 | 16 | 30 | 13 |
4 | 12 | 8 | 11 | 27 | 19 | 14 |
5 | 0 | 7 | 10 | 21 | 10 | 32 |
6 | 0 | 0 | 0 | 6 | 11 | 13 |
解:
一、问题分析
根据第一题的题意我们可以知道,此题的最终目标是让我们建立一种数学模型来解决这个实际生活中的问题,此题意简而言之就是为了解决6个人做6项工作的指派最优问题,从而使题目中的收益等达到所需要的目的。在题目中曾提到:每个人完成一项工作。其意思就是每人只能做一项工作且每项工作只能做一人做。
二、符号说明
此题属于最优指派问题,引入如下变量:
题目中说:表示第i个人做第j项工作的收益。例如则表示第5个人做第6项工作。
即
s.t.:
,j=1,2,3,···,6
,i=1,2,3,···,6
,i,j=1,2,3,···,6
此题需要求出最大值最优(最大值),即需要使用max,表示最大。
在编程过程中“@bin(x)”是“限制x为0或1”。
三、建立模型
此题属于最优指派问题,与常见的线性问题极为类似。因此,使用Lingo软件。
由于“每人只能做一项工作且每项工作只能做一人做”故采用0-1规划求得优。
四、模型求解
(一)常规程序求解
Lingo输入框:
max=20*c11+15*c12+16*c13+5*c14+4*c15+7*c16+
17*c21+15*c22+33*c23+12*c24+8*c25+6*c26+
9*c31+12*c32+18*c33+16*c34+30*c35+13*c36+
12*c41+8*c42+11*c43+27*c44+19*c45+14*c46+
0*c51+7*c52+10*c53+21*c54+10*c55+32*c56+
0*c61+0*c62+0*c63+6*c64+11*c65+13*c66;
c11+c12+c13+c14+c15+c16=1;
c21+c22+c23+c24+c25+c26=1;
c31+c32+c33+c34+c35+c36=1;
c41+c42+c43+c44+c45+c46=1;
c51+c52+c53+c54+c55+c56=1;
c61+c62+c63+c64+c65+c66=1;
c11+c21+c31+c41+c51+c61=1;
c12+c22+c32+c42+c52+c62=1;
c13+c23+c33+c43+c53+c63=1;
c14+c24+c34+c44+c54+c64=1;
c15+c25+c35+c45+c55+c65=1;
c16+c26+c36+c46+c56+c66=1;
@bin(c11);@bin(c12);@bin(c13);@bin(c14);@bin(c15);@bin(c16);
@bin(c21);@bin(c22);@bin(c23);@bin(c24);@bin(c25);@bin(c26);
@bin(c31);@bin(c32);@bin(c33);@bin(c34);@bin(c35);@bin(c36);
@bin(c41);@bin(c42);@bin(c43);@bin(c44);@bin(c45);@bin(c46);
@bin(c51);@bin(c52);@bin(c53);@bin(c54);@bin(c55);@bin(c56);
@bin(c61);@bin(c62);@bin(c63);@bin(c64);@bin(c65);@bin(c66);
Lingo输出(结果)框:
Global optimal solution found.
Objective value: 142.0000
Extended solver steps: 0
Total solver iterations: 0
Variable Value Reduced Cost
C11 1.000000 -20.00000
C12 0.000000 -15.00000
C13 0.000000 -16.00000
C14 0.000000 -5.000000
C15 0.000000 -4.000000
C16 0.000000 -7.000000
C21 0.000000 -17.00000
C22 0.000000 -15.00000
C23 1.000000 -33.00000
C24 0.000000 -12.00000
C25 0.000000 -8.000000
C26 0.000000 -6.000000
C31 0.000000 -9.000000
C32 0.000000 -12.00000
C33 0.000000 -18.00000
C34 0.000000 -16.00000
C35 1.000000 -30.00000
C36 0.000000 -13.00000
C41 0.000000 -12.00000
C42 0.000000 -8.000000
C43 0.000000 -11.00000
C44 1.000000 -27.00000
C45 0.000000 -19.00000
C46 0.000000 -14.00000
C51 0.000000 0.000000
C52 0.000000 -7.000000
C53 0.000000 -10.00000
C54 0.000000 -21.00000
C55 0.000000 -10.00000
C56 1.000000 -32.00000
C61 0.000000 0.000000
C62 1.000000 0.000000
C63 0.000000 0.000000
C64 0.000000 -6.000000
C65 0.000000 -11.00000
C66 0.000000 -13.00000
Row Slack or Surplus Dual Price
1 142.0000 1.000000
2 0.000000 0.000000
3 0.000000 0.000000
4 0.000000 0.000000
5 0.000000 0.000000
6 0.000000 0.000000
7 0.000000 0.000000
8 0.000000 0.000000
9 0.000000 0.000000
10 0.000000 0.000000
11 0.000000 0.000000
12 0.000000 0.000000
13 0.000000 0.000000
(二)循环语句求解
Lingo输入框:
model:
sets:
gz/A1..A6/:a;
ry/B1..B6/:b;
yw(gz,ry):xy,x;
endsets
data:
a=1,1,1,1,1,1;
b=1,1,1,1,1,1;
xy=20 15 16 5 4 7,
17 15 33 12 8 6,
9 12 18 16 30 13,
12 8 11 27 19 14,
0 7 10 21 10 32,
0 0 0 6 11 13;
enddata
max=@sum(yw:xy*x);
@for(gz(i):@sum(ry(j):x(i,j))=1);
@for(ry(j):@sum(gz(i):x(i,j))=1);
@for(yw(i,j):@bin(x(i,j)));
End
Lingo输出(结果)框
Global optimal solution found.
Objective value: 142.0000
Extended solver steps: 0
Total solver iterations: 0
Variable Value Reduced Cost
A( A1) 1.000000 0.000000
A( A2) 1.000000 0.000000
A( A3) 1.000000 0.000000
A( A4) 1.000000 0.000000
A( A5) 1.000000 0.000000
A( A6) 1.000000 0.000000
B( B1) 1.000000 0.000000
B( B2) 1.000000 0.000000
B( B3) 1.000000 0.000000
B( B4) 1.000000 0.000000
B( B5) 1.000000 0.000000
B( B6) 1.000000 0.000000
XY( A1, B1) 20.00000 0.000000
XY( A1, B2) 15.00000 0.000000
XY( A1, B3) 16.00000 0.000000
XY( A1, B4) 5.000000 0.000000
XY( A1, B5) 4.000000 0.000000
XY( A1, B6) 7.000000 0.000000
XY( A2, B1) 17.00000 0.000000
XY( A2, B2) 15.00000 0.000000
XY( A2, B3) 33.00000 0.000000
XY( A2, B4) 12.00000 0.000000
XY( A2, B5) 8.000000 0.000000
XY( A2, B6) 6.000000 0.000000
XY( A3, B1) 9.000000 0.000000
XY( A3, B2) 12.00000 0.000000
XY( A3, B3) 18.00000 0.000000
XY( A3, B4) 16.00000 0.000000
XY( A3, B5) 30.00000 0.000000
XY( A3, B6) 13.00000 0.000000
XY( A4, B1) 12.00000 0.000000
XY( A4, B2) 8.000000 0.000000
XY( A4, B3) 11.00000 0.000000
XY( A4, B4) 27.00000 0.000000
XY( A4, B5) 19.00000 0.000000
XY( A4, B6) 14.00000 0.000000
XY( A5, B1) 0.000000 0.000000
XY( A5, B2) 7.000000 0.000000
XY( A5, B3) 10.00000 0.000000
XY( A5, B4) 21.00000 0.000000
XY( A5, B5) 10.00000 0.000000
XY( A5, B6) 32.00000 0.000000
XY( A6, B1) 0.000000 0.000000
XY( A6, B2) 0.000000 0.000000
XY( A6, B3) 0.000000 0.000000
XY( A6, B4) 6.000000 0.000000
XY( A6, B5) 11.00000 0.000000
XY( A6, B6) 13.00000 0.000000
X( A1, B1) 1.000000 -20.00000
X( A1, B2) 0.000000 -15.00000
X( A1, B3) 0.000000 -16.00000
X( A1, B4) 0.000000 -5.000000
X( A1, B5) 0.000000 -4.000000
X( A1, B6) 0.000000 -7.000000
X( A2, B1) 0.000000 -17.00000
X( A2, B2) 0.000000 -15.00000
X( A2, B3) 1.000000 -33.00000
X( A2, B4) 0.000000 -12.00000
X( A2, B5) 0.000000 -8.000000
X( A2, B6) 0.000000 -6.000000
X( A3, B1) 0.000000 -9.000000
X( A3, B2) 0.000000 -12.00000
X( A3, B3) 0.000000 -18.00000
X( A3, B4) 0.000000 -16.00000
X( A3, B5) 1.000000 -30.00000
X( A3, B6) 0.000000 -13.00000
X( A4, B1) 0.000000 -12.00000
X( A4, B2) 0.000000 -8.000000
X( A4, B3) 0.000000 -11.00000
X( A4, B4) 1.000000 -27.00000
X( A4, B5) 0.000000 -19.00000
X( A4, B6) 0.000000 -14.00000
X( A5, B1) 0.000000 0.000000
X( A5, B2) 0.000000 -7.000000
X( A5, B3) 0.000000 -10.00000
X( A5, B4) 0.000000 -21.00000
X( A5, B5) 0.000000 -10.00000
X( A5, B6) 1.000000 -32.00000
X( A6, B1) 0.000000 0.000000
X( A6, B2) 1.000000 0.000000
X( A6, B3) 0.000000 0.000000
X( A6, B4) 0.000000 -6.000000
X( A6, B5) 0.000000 -11.00000
X( A6, B6) 0.000000 -13.00000
Row Slack or Surplus Dual Price
1 142.0000 1.000000
2 0.000000 0.000000
3 0.000000 0.000000
4 0.000000 0.000000
5 0.000000 0.000000
6 0.000000 0.000000
7 0.000000 0.000000
8 0.000000 0.000000
9 0.000000 0.000000
10 0.000000 0.000000
11 0.000000 0.000000
12 0.000000 0.000000
13 0.000000 0.000000
五、模型结果
通过以上的应用Lingo模型求解,得出结论:
第1项工作由第1个人来完成。
第2项工作由第3个人来完成。
第3项工作由第5个人来完成。
第4项工作由第4个人来完成。
第5项工作由第6个人来完成。
第6项工作由第2个人来完成。
| 甲 | 乙 | 丙 | 丁 |
A | 2 | 9 | 10 | 7 |
B | 1 | 3 | 4 | 2 |
C | 8 | 4 | 2 | 5 |
D | 3 | 8 | 4 | 6 |
四、上机实验内容。
用电子表格求解下属运输问题:某公司设有A,B,C三个加工厂,产量分别为:9吨、5吨、7吨;有甲,乙,丙,丁四个销售点,销量分别为:3吨、8吨、4吨、6吨;从各工厂到销售点的单位产品的运价为左表所示,问该公司应该如何调运产品使总运费最少?
【实验报告】
上机实验内容。
实验六 网络最大流
(设计性实验,1学时)
【实验目的与要求】
1. 掌握网络最大流模型;
2. 建立模型,用lingo求解网络最大流问题。
【实验仪器、器材与试剂】
无
【实验内容、方法与步骤】
最大流问题:
将石油从城市s经由4个中转站运向t,各城市连接及管道容量如下图,求解从s到t的最大流。

Lingo求解程序:
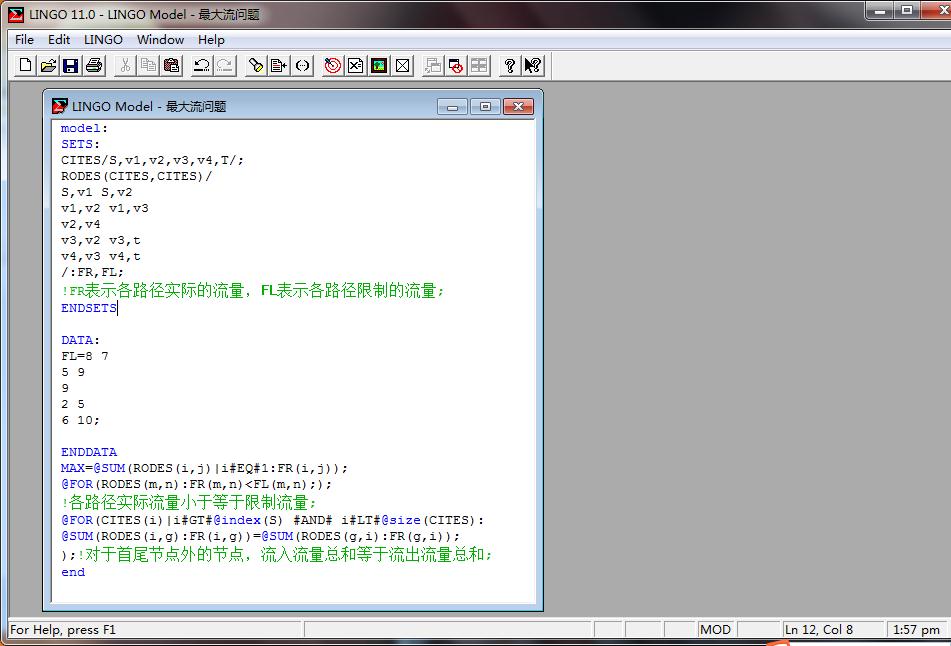
Lingo程序运行结果:
求解得到全局最优解,最大流为14,其中各个路径上的明细流量详见下图中的FR值。
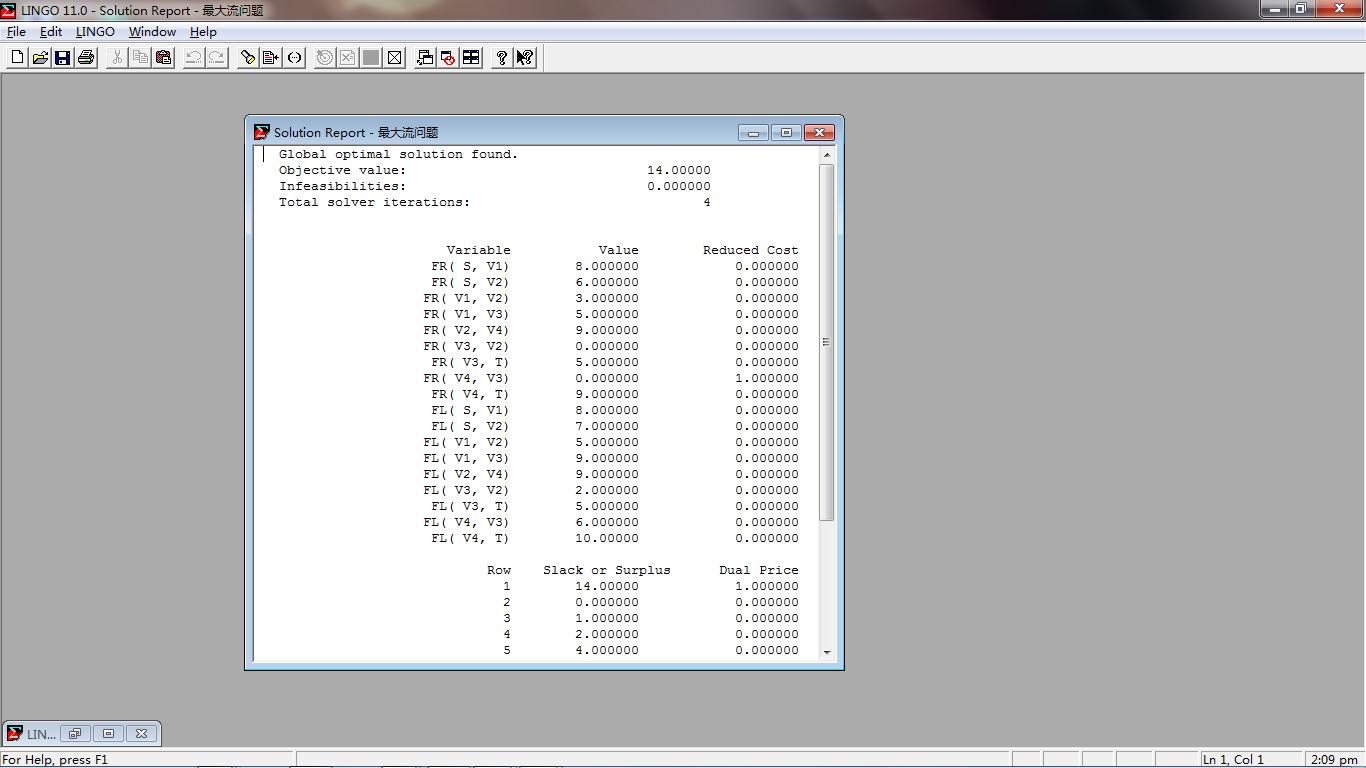
【实验报告】
学号姓名提交课后的习题实验报告。
